Пирамида призмамен бірге үш өлшемді кеңістіктегі тамаша көпбұрыш, олардың геометриялық сипаттамалары орта мектепте оқытылады. Бұл мақалада біз пирамидалардың не екенін, олар қандай элементтерден тұратынын қарастырамыз, сонымен қатар дұрыс пирамидаларды қысқаша сипаттаймыз.
Геометриялық фигуралар пирамидасы
Геометрия тұрғысынан пирамида бір көпбұрыш пен бірнеше үшбұрыштан тұратын кеңістіктік фигура. Бұл фигураны алу өте қарапайым. Ол үшін n қабырғасы бар көпбұрышты алып, одан кейін көпбұрыш жазықтығында жатпайтын кеңістіктегі ерікті нүктені таңдап, көпбұрыштың әрбір төбесін осы нүктеге қосыңыз. Осылайша жасалған фигура бір төбесінде бір-бірімен қосылған n үшбұрыштан тұратыны анық.
Сипатталған фигураның геометриялық пішінін елестету үшін суретке түсірейік.

Бұл төртбұрышты пирамиданы көрсетеді, оның негізітөртбұрыш, ал бүйір беті ортақ төбесі бар төрт үшбұрыштан тұрады.
Пирамида элементтері
Кез келген көпбұрыштар сияқты пирамида үш түрлі элементтерден тұрады:
- шеттері;
- топтар;
- қабырға.
Беттер - фигураның ішкі көлемін қоршаған кеңістіктен бөлетін жазықтықтардың бөліктері. Егер пирамиданың табанында n-бұрыш болса, онда оның беттерінің саны әрқашан n+1 болады. Олардың n қабырғасы үшбұрышты және бір қабырғасы аталған n бұрыштық негіз болып табылады.
Шыңдар - фигураның үш немесе одан да көп беттері қиылысатын нүктелер. Негізгі аймақ әрқайсысы екі үшбұрышты бет пен негізден құралған n шыңнан тұрады. Үшбұрышты n қабырғаның түйіскен нүктесі пирамиданың төбесі деп аталады. Осылайша, қарастырылып отырған фигура n+1 шыңдардан тұрады.
Шеттері - екі бет қиылысқан кезде пайда болатын түзу сызықтар. Әрбір жиек оның ұштарында екі төбемен шектелген. Негізі n-бұрышты кез келген пирамиданың 2n шеттері бар. Бұл санның жартысы, яғни n тек қана бүйірлік үшбұрыштардың қиылысуынан құралады.
Фигураның мүмкін түрлері
Қарастырылып отырған фигураның аты негізіндегі көпбұрыш түрі бойынша бірегей түрде анықталады. Мысалы, оның үш бұрышы және үш қабырғасы болса, пирамида үшбұрышты, төртеуі болса төртбұрышты және т.б. болады.
Көпбұрыш дөңес және ойыс, сондай-ақ қалыпты және жалпы түрі болуы мүмкін. Мұның бәрі пирамиданың сыртқы түрін де анықтайды.
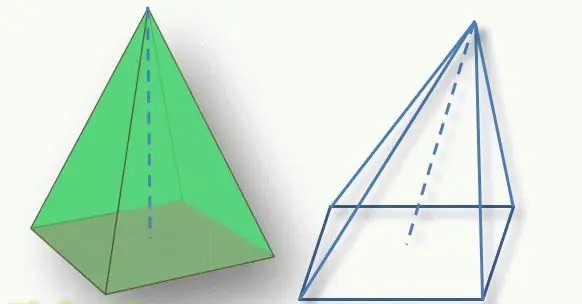
Фигураның түрін анықтаудағы маңызды сәт пирамиданың төбесінің оның табанына қатысты орналасуы болып табылады. Жоғарыдан көпбұрышты табанға жүргізілген перпендикуляр кесінді фигураның биіктігі деп аталады. Егер бұл кесінді негізді өзінің геометриялық центрінде қиып өтсе (үшбұрыш үшін бұл медианалардың қиылысы, төртбұрыш үшін диагональдардың қиылысы), онда фигураны түзу деп атайды. Әйтпесе, олар көлбеу пирамида туралы айтады.
Егер табанының n-бұрышы дұрыс (теңбүйірлі үшбұрыш, шаршы, т.б.) және фигура түзу болса, онда ол дұрыс пирамида деп аталады.
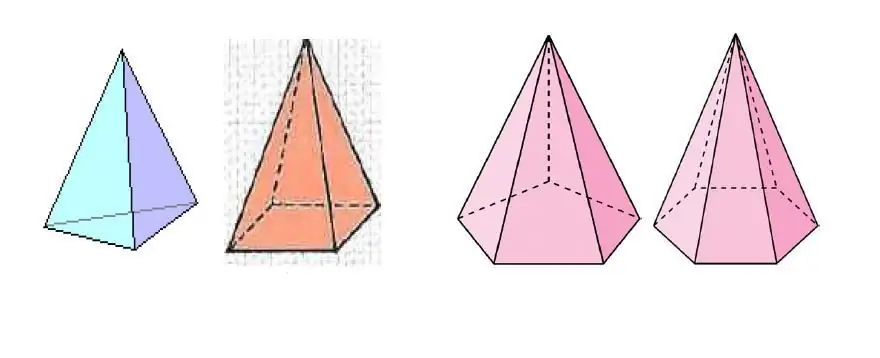
Жоғарыдағы суретте негізінде көпбұрыштың қабырғаларының саны бойынша ерекшеленетін бірнеше пирамидалар көрсетілген.
Тұрақты пирамидалардың қасиеттері
Бұл пирамидалар осы класстың басқа фигураларынан симметрияның жоғары дәрежесімен ерекшеленеді. Осыған байланысты олармен әртүрлі геометриялық есептеулерді жүргізу ыңғайлы, мысалы, көлем немесе бет ауданы.
Тұрақты пирамиданың табанында n-бұрышы бар, оның ауданы оның қабырғасының ұзындығын білу арқылы ерекше анықталады. Фигураның бүйір беті тең бүйірлі n бірдей үшбұрыштардан тұрады. Бүйір бетінде орналасқан дұрыс пирамиданың шеттері бір-біріне тең. Бұл жиектің ұзындығының мәні фигураның апотемасын есептеу және бетінің ауданын анықтау кезінде жиі пайдаланылады.
Дұрыс пирамиданың биіктігі - фигураның екінші маңызды сипаттамасы (бірінші - жиектің ұзындығынегіздер). Дыбыс деңгейін есептеу кезінде биіктік пайдаланылады.
Пирамиданың бүйір беттерін қиып өтетін табанға параллель кез келген жазықтық көпбұрышты қиманың пайда болуына әкеледі. Ол негізгі көпбұрышқа қатысты гомотетикалық. Сипатталған кесінді операциясы жаңа фигуралардың тұтас класының - қиылған кәдімгі пирамидалардың қалыптасуына әкеледі.
Ең атақты пирамидалар

Әрине, бұл Мысыр перғауындарының кәдімгі төртбұрышты пирамидалары. Гиза деп аталатын жерде бұл тас ескерткіштердің 100-ден астамы бар, олардың дизайнының кемелдігі мен геометриялық параметрлерінің дәлдігі күні бүгінге дейін ғалымдарды таң қалдыруда. Олардың ең үлкені - биіктігі шамамен 146 метр және ұзындығы шамамен 230 метр болатын Хеопс пирамидасы.
Бұл пирамидалардың нақты не үшін қызмет еткенін, сондай-ақ қандай механизмдермен және қашан салынғанын күні бүгінге дейін ешкім білмейді.






