Математикада қосынды (грекше үлкен сигма таңбасымен белгіленеді) - сандардың қосындыларының жиынтығы. Сома қанша? Бұл осындай әрекеттің нәтижесі. Егер сандар солдан оңға қарай бірінен соң бірі қосылса, аралық нәтиже жартылай қосынды болады.
Сома қандай?
Қосындыланатын сандар бүтін, рационал, нақты немесе күрделі болуы мүмкін. Оларға қосымша мәндердің басқа түрлерін қосуға болады: векторлар, матрицалар, көпмүшелер және жалпы кез келген аддитивті топтың элементтері (немесе тіпті моноид).
Егер терминдер элементтерінің саны шекті болса, онда қосынды әрқашан нақты анықталған мән береді. Мәндердің шексіз тізбегінің қосындысы қатар деп аталады. Оның мәнін жиі шектеу арқылы анықтауға болады (бірақ кейде мән шексіз болуы мүмкін).
Тізімдер
Сандардың қосындысын [3, 7, 2, 1] мәні оған енгізілген цифрлардың қосындысы болатын өрнек арқылы анықтауға болады, мысалы 3 + 7 + 2 + 1=13. қосуассоциативті түрде қосынды терминдердің қалай топтастырылғанына байланысты емес, мысалы, (3 + 7) + (2 + 1) және 3 + ((7 + 2) + 1) екеуі де тоғызға тең, сондықтан жақша әдетте алынып тасталады.. Қосу да ауыспалы болып табылады, сондықтан терминдерді қайта орналастыру қосындының мәнін өзгертпейді. Бұл сипат шексіз жинақтау үшін жұмыс істемеуі мүмкін екенін ескеріңіз.

Осындай реттіліктерді қосу үшін арнайы белгілер жоқ. Екі элементтен аз болса, шамалы нюанс бар. Бір мүшенің тізбегінің қосындысы қосу белгісін қамтымайды (ол санның өзінен айырмашылығы жоқ), ал егер мүлде элементтер болмаса, онда оны жазуға да болмайды (бірақ оның орнына оны былай белгілеуге болады). оның мәні «0»). Дегенмен, реттілік шарттары функция сияқты белгілі бір үлгімен көрсетілсе, онда қосу операторы пайдалы немесе тіпті маңызды болуы мүмкін.
Жазба
Қосындының не екенін түсіну үшін оның сыртқы түрін талдау керек.
1-ден 100-ге дейінгі бүтін сандар тізбегін қосу үшін жетіспейтін мүшелерді көрсету үшін эллипсті қамтитын өрнек жиі пайдаланылады: 1 + 2 + 3 + 4 + … + 99 + 100. Үлгі: бұл мысалда көру өте оңай. Дегенмен, күрделірек опциялар үшін элементтердің мәнін табу үшін қолданылатын ережені нақты көрсету қажет, оған «Σ» қосу операторы арқылы қол жеткізуге болады. Осы таңбаны (сигма) пайдаланып, келесі белгіні қолдануға болады:
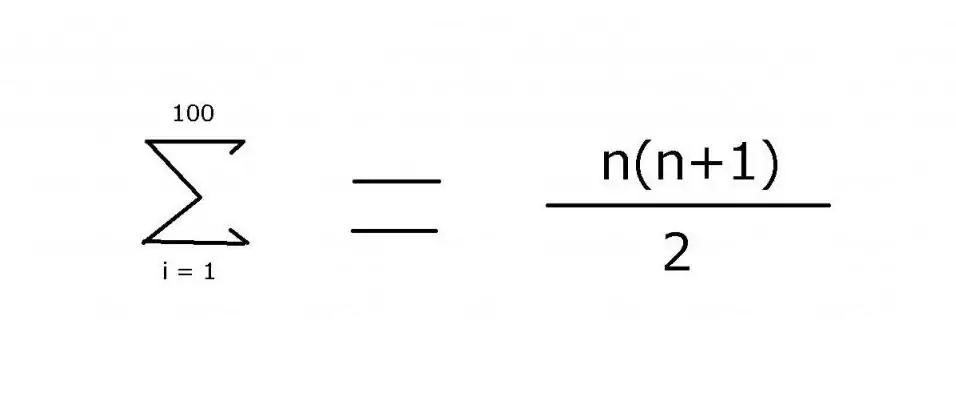
Бұл өрнектің мәні 5050. Оны формуланың екінші бөлігі шыққан математикалық индукция арқылы табуға болады.
Әртүрлі реттіліктер үшін формула өзгереді. Жазу процесі қандай да бір шексіз дәйектіліктің алдын ала кескінін іздеуге, содан кейін оны формуламен сипаттауға дейін қысқарады. Бұл әрекетті орындағаннан кейін белгілі бір жағдайда қандай сома екенін түсіну қиын емес.
Сандардың таңбаларымен (плюс немесе минус) қосылатынын нақтылау қажет болғанда алгебралық қосынды термині қолданылады. Мысалы, электр тізбегінің теориясында Кирхгофтың тізбек заңдары түйінге кіретін және шығатын токтарға қарама-қарсы белгілер беретін бір нүктеде түйісетін өткізгіштер желісіндегі токтардың алгебралық қосындысын қарастырады.






